Coriolis flow measuring principle
Understanding the principle, applications and benefits of Coriolis flowmeters
In brief
- Coriolis mass flowmeters are widely used in the chemical and food processing industries, where mass flow measurement is preferred over volume due to its stability under varying physical conditions. This is particularly important for accurate fiscal metering.
- The Coriolis principle, named after Gaspard-Gustave de Coriolis, measures mass flow directly by using the Coriolis force. This force, occurring in rotating systems, causes a measurable twist in oscillating measuring tubes.
- Coriolis flowmeters are versatile and available in various designs and sizes. They can measure additional parameters like density and temperature, making them suitable for applications from pharmaceutical dosing to ship cargo loading. They offer benefits such as easy
cleaning, low pressure loss, and high accuracy. - Coriolis meters high accuracy make them ideal for fiscal metering.
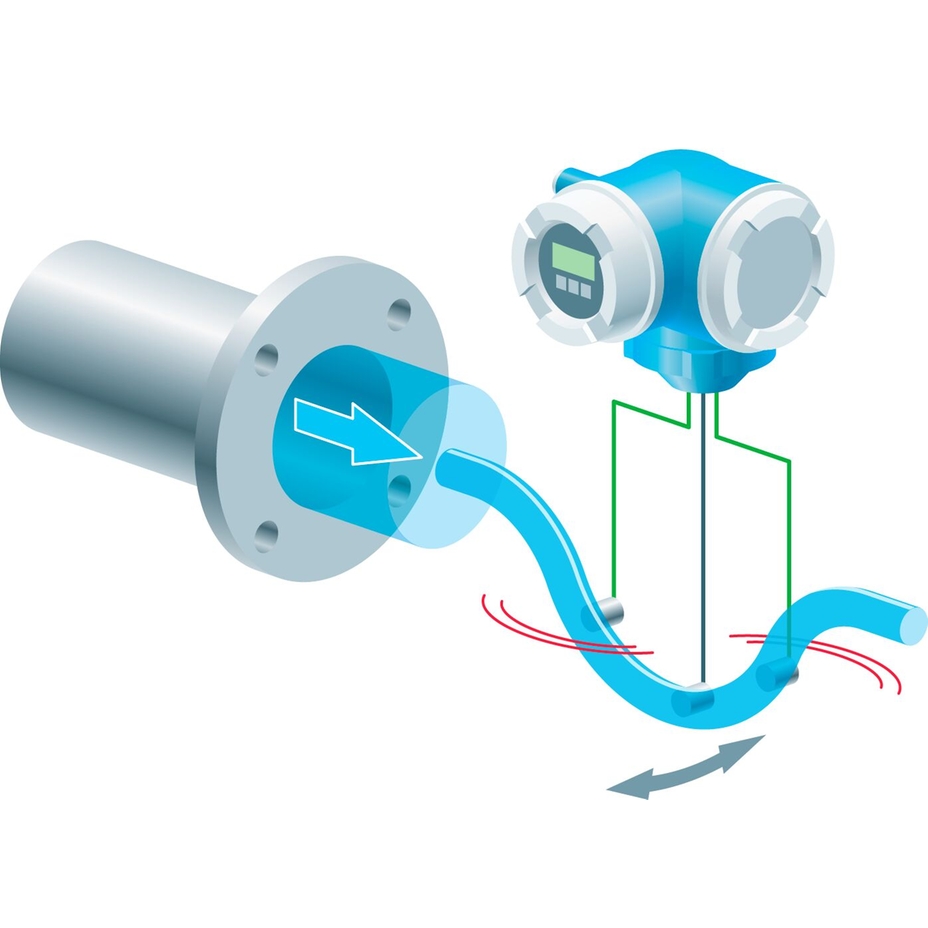
Measuring principle of Coriolis mass flowmeters
In many sectors of industry, it is mass flow measurement rather than volume flow that has to be measured. In food processing, for example, products such as pastes, pulps and yogurt are generally batched by weight, not volume. Therefore, the label on the packaging tells the consumer the weight of the product instead of the volume. One reason for this is that the volume of most fluids can vary widely under physical influences such as pressure, temperature and density. The mass of a fluid is not affected by these influences – so mass flow measurement has some advantages that volumetric measurement simply cannot match. This is an aspect of particular importance for fiscal metering in batching and metering fluids.
The mass of a body is generally determined by weighing. From the engineering point of view, however, there are major difficulties to be overcome when directly weighing a mass that is flowing continuously through a piping system. This is the reason why recent decades have seen the emergence of a measuring principle that enables mass flow in pipes to be measured directly and continuously – namely mass flow measurement by the Coriolis principle. In some applications it makes more sense to apply this Coriolis principle than to determine mass indirectly by measuring volume flow and density (volume × density = mass).
The Coriolis measuring principle
The earliest description of this principle is generally attributed to the French physicist and mathematician whose name it now bears, Gaspard-Gustave de Coriolis (1792 – 1843).
The effect occurs only in rotating systems, for example on fairground merry-go-rounds or on our rotating planet, but it should not be confused with centrifugal force. Despite the fact that the term “Coriolis force” is in widespread use, it is frequently difficult to describe the force, much less explain it. Its occurrence is always to be observed when straight movement and rotary action are superimposed in a system.
A practical example is illustrated in Figure 1: A person standing still on a rotating turntable has only to lean slightly inward to counteract centrifugal force (left). A person moving from the center of rotation toward the edge of the turntable, however, encounters steadily increasing rotational speed and, as inertia comes into play, has to overcome a force known as the Coriolis force. This Coriolis force acts to deflect the person from the shortest route across the turntable (straight along the radius). The heavier the person, the faster the speed of rotation, and the faster the person walks toward the circumference (“mass flow”), the more inertia is perceptible and the more powerful is the effect of the Coriolis force.
In mathematical terms, the Coriolis force (FC) is therefore proportional to the moving mass (m· ), speed of rotation (ω) and radial velocity (vr) in the rotating system:
Fc = 2 ⋅ m ⋅ ω ⋅ vr
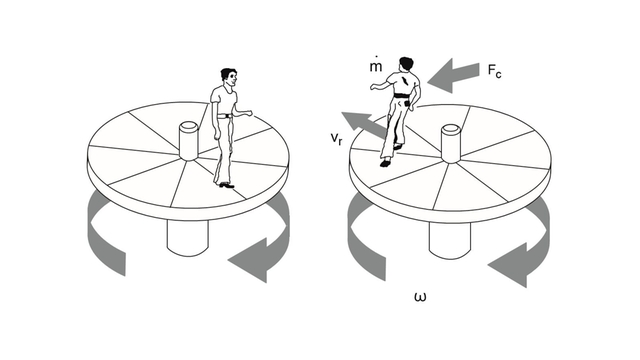
Fig. 1: Origin and effects of the Coriolis force on a rotating turntable.
Coriolis forces are always present when linear movement and rotary action are superimposed within a system (Fig. 1, right). In the absence of linear movement (Fig. 1, left, person standing still), only centrifugal forces occur.
In a
Endnotes
We value your privacy
We use cookies to enhance your browsing experience, collect statistics to optimize site functionality, and deliver tailored advertisements or content.
By selecting "Accept all", you consent to our use of cookies.
For further details please review our privacy policy .









